O átomo de hidrogênio ocupa um certo volume no espaço; obviamente o elétron acha-se completamente contido neste volume, e como consequência disto, a probabilidade, ou melhor, a probabilidade total de encontrarmos este elétron neste dado volume é máxima, isto é, se calcularmos esta probabilidade ela deverá ser igual à unidade. Vimos que, sendo Ψ_nlm a função de onda que representa o comportamento do elétron do átomo de hidrogênio, então a probabilidade total de encontrarmos o elétron do hidrogênio (na região do espaço que o átomo existe) é definida como:

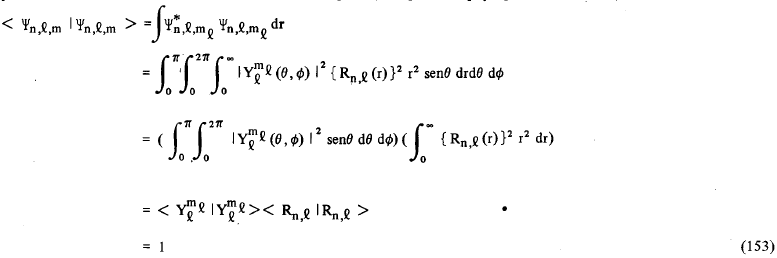
Na integral (153), dr representa o elemento de volume em coordenadas polares esféricas, isto é, dr = r² sen(θ) dr dθ dφ. Muitas vezes nós representamos o elemento de volume por dv ao invés de dr. Se, ao invés da probabilidade total nós quisermos calcular a probabilidade de encontrar o elétron em uma dada região do espaço compreendida entre r e r + dr; θ e θ + dθ; e φ e φ + dφ; basta calcularmos

Esta fórmula é exatamente equivalente ao integrando da equação (153), e corresponde à probabilidade de encontrarmos o elétron no elemento de volume dr= r² sen(θ) dr dθ dφ.

Tabela 2. Funções Reais para o elétron do átomo de hidrogênio.

Por outro lado, a probabilidade de encontrarmos um elétron numa região esférica tendo o núcleo como centro das coordenadas r e de raio externo r + dr, e independente de θ e φ, é dada por

À função {R_n,l(r)}².r² dá-se o nome de Função de Distribuição Radial, D(r); {R_n,l(r)}².r² nos dá a probabilidade de encontrar o elétron a uma distância r do núcleo.

Fig. 6. Função de distribuição radial D(r), para o átomo de hidrogênio para valores de m = 1, 2 e 3. A seta indica o valor de <r>_nlm.

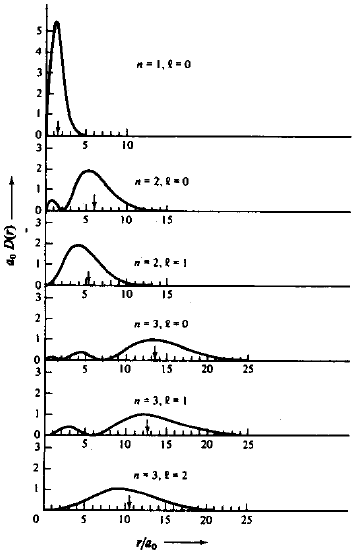
A função D(r) representa a probabilidade de encontrarmos o elétron à uma dada distância r do núcleo. Analisando o comportamento de D(r), para o elétron no orbital 1s, veremos que à medida que fazemos r variar de zero a ∞, D(r) que inicialmente é zero, passa por um máximo para depois decair novamente para zero. O valor de r para o qual D(r) é máxima, corresponde exatamente ao valor de r que mais contribui para o valor médio < r >. Este valor de r para o qual D(r) é máxima, corresponde ao “raio de Bohr”, que aliás difere do valor esperado < r > ou valor médio de r no estado fundamental. O ponto em que D(r) passa por um máximo pode ser calculado facilmente, pois neste ponto d / dr {D(r)} = 0. Assim, para o orbital 1s, teremos que

Isto quer dizer que a função de distribuição radial, para o H no estado 1s, passa por um máximo no ponto em que r = 0,529_A^o; este valor é exatamente igual ao valor calculado por Bohr. Note que o elétron do átomo de Bohr circulava numa órbita plana de raio r = 0,529_A^o, enquanto que neste caso temos simetria esférica. A diferença entre o valor médio de r e o valor de r = a₀ determinado por Bohr, pode ser demonstrada facilmente. Como a função de onda para o hidrogênio é normalizada, o valor esperado ou valor médio para o raio r do átomo de hidrogênio quando está no estado fundamental (i. e., 1s), é dado por (vide postulado V).

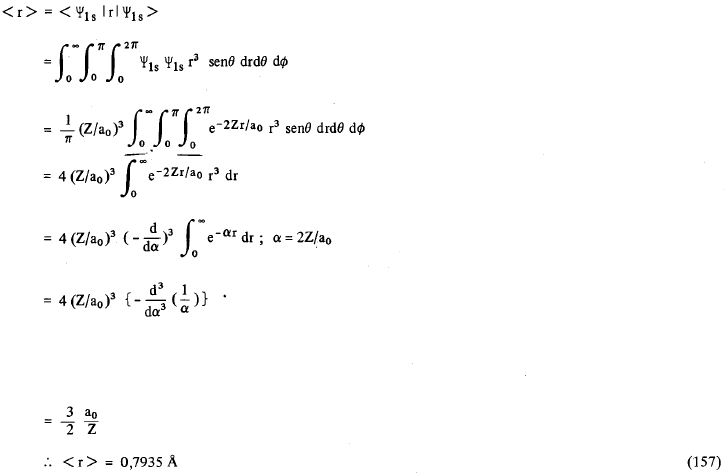
Isto quer dizer que se determinarmos r experimentalmente, isto é, se pudermos medir o “raio” do átomo de hidrogênio no estado fundamental (orbital 1s), veremos que este valor experimental coincide com < r >= 0,793_A^o e não com 0,529_A^o. De uma maneira geral, o valor médio de r, isto é < r >_n,l é dado por

Assim, analisando (158) nós vemos que em média quanto maior for o número quântico principal n, mais afastado do próton estará o elétron. No estado fundamental do hidrogênio (n = 1, l = 0), o elétron encontra-se em média a 3/2 a₀ do núcleo, o que está de acordo com o que já havíamos calculado anteriormente.

Inicialmente nós havíamos definido Ψ como um produto das funções R, Θ e Φ. Sendo assim, fazendo uso de (68), (95) e (137), nós podemos definir a função de onda eletrônica do átomo de hidrogênio, como:

ou ainda

onde as funções Y_l,m (θ,φ) são conhecidas como Harmônicos Esféricos, e definidas como

Como os conjuntos de funções {Φ_m}, {Θ_l,m} e {R_n,l} são ortogonais, então a função Ψ será também ortogonal.

Resumindo estas propriedades, teremos:

Agora que conhecemos a solução da Equação de Schrödinger para o átomo de hidrogênio, já estamos em condições de definir e estudar uma série de propriedades relacionadas com o mesmo. As funções de onda para o hidrogênio (ou para átomos ou íons atômicos com um único elétron) são definidas através de (138) fórmula geral para Ψ_nlm. Cada conjunto de n, l, m define uma função de onda, que por sua vez representa um dado estado eletrônico do átomo. Quando n é igual a um, nós dizemos que o elétron está na camada K. As camadas eletrônicas K, L, M, etc., correspondem respectivamente a n = 1,2,3 etc. As funções de onda de um único elétron são comumente chamadas de orbitais. Assim, não é correto referir-se a “orbitais de dois elétrons”. Orbitais correspondentes a l = 0, 1, 2, 3, 4, 5 etc, são conhecidos respectivamente, por orbitais s, p, d, f, g, h, etc., omitindo-se somente a letra j. Assim, a função de onda correspondente a n=2, l = 1, m = 0 é representada por Ψ_2,1,0 ou simplesmente, função 2p. A designação destas letras (s, p, d, f, g, etc.) prende-se à terminologia inglesa utilizada por espectroscopistas que distinguiam linhas espectrais pelo seu aspecto, isto é, s → sharp, p → principal, d → difuse e f → fine. As outras foram sugeridas como extensão da nomenclatura, mantendo a ordem alfabética.

Na Tabela 1 nós temos as fórmulas de algumas funções de onda eletrônicas para estados estacionários do hidrogênio.

Tabela 1 - Funções de onda para o hidrogênio. Nestas equações  σ = nρ / 2 = Zr/a₀.  Os sinais superiores e inferiores nos índices de Ψ devem corresponder respectivamente aos sinais superiores ou inferiores da parte exponencial das fórmulas. Neste caso, todos os índices positivos de Ψ correspondem  a exp(imφ) e os negativos correspondem a exp(-imφ).  

Figura 4 - Gráficos polares dos Harmônios Esféricos para l = 0, 1, 2  para todos os valores do índice m e para φ = 0. A linha tracejada indica o eixo z.  

Através da equação (138) que define Ψ_nlm nós podemos notar que, com exceção dos casos em que m = 0, todas as funções hidrogênicas são complexas, isto é, possuem uma parte imaginária, não nula, Comumente, quando discutimos os problemas relacionados com estrutura atômica, molecular e ligações químicas, utilizamos funções hidrogênicas reais obtidas pela combinação linear destas funções complexas. Assim, para n = 2 e l = 1 podemos definir as funções reais Ψ_2px, Ψ_2py e  Ψ_2pz como

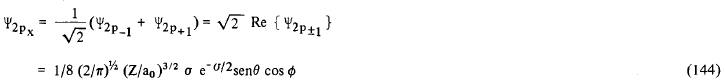
O fator de 1 / √2 que aparece nas definições de 2p_x e 2p_y é simplesmente uma constante de normalização que poderia ser calculada facilmente, caso nós não a tivéssemos definido de antemão. Para tal, bastaria escrevermos Ψp_x, como

e calcular o produto escalar impondo a condição de que < Ψ_2px | Ψ_2py> = 1. Assim, lembrando que as funções Ψ_n,l,m. São ortonormalizadas, isto é

teremos que

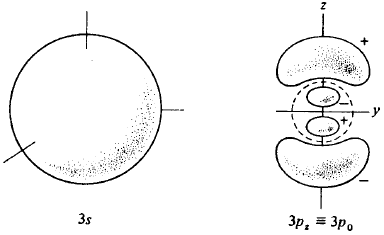
Fig. 5. Formato de alguns orbitais atômicos do átomo de hidrogênio. O orbital 2s tem um modo esférico que não aparece na figura; O orbital 3s tem dois destes modos. O orbital 3p, tem um modo esférico (indicado pela linha tracejada) e um plano modal (o plano xy). O orbital 3d_z² tem dois cones modais e o 3d_x²-y² tem dois planos modais. Na figura nós indicamos os sinais relativos de cada função de onda.

Existe uma razão muito simples para a designação destas funções como 2p_x, 2p_y e 2p_z. Lembrando que podemos reescrever as funções Ψ_2px, Ψ_2py e Ψ_2pz como

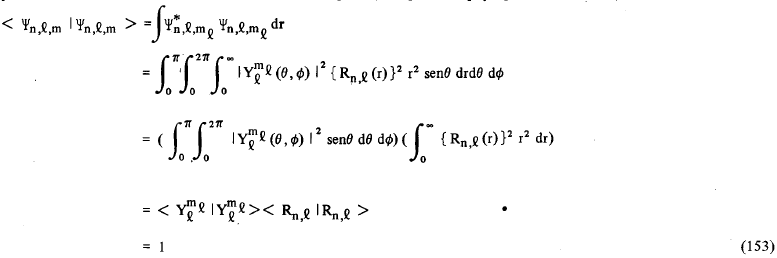
Note que x, y e z aparecem respectivamente nas definições de 2p_x, 2p_y e 2p_z, dando origem a esta notação. As fórmulas para algumas destas funções reais, desde 1s até 3d_xy, são dadas na Tabela 2, na qual explicitamos ao lado de cada uma a sua dependência com as coordenadas cartesianas a fim de tornar mais claro o simbolismo empregado.

 A função R(r) é a solução da equação diferencial (64) e nos dá a dependência radial da função de onda do átomo de hidrogênio. Se nesta equação substituirmos a constante b pelo seu valor, então (64) pode ser reescrita como

ou então

Para resolvermos esta equação, convém efetuarmos algumas mudanças de variáveis, definindo

onde n é uma constante qualquer, a ser determinada, utilizando (99) nós podemos reescrever (98) como:

Para resolvermos a equação diferencial (100) nós utilizaremos um método diferente daqueles empregados para as equações em θ e φ. Neste caso nós iniciaremos o nosso estudo fazendo uma análise do comportamento assintótico (para valores grandes de p) da equação radial; assim, no limite do p →∞, a equação diferencial (100) reduz-se a

cujas soluções são

Considerando que um átomo é finito, então a função R_l(p) deve ser tal que

Obviamente, quando esta condição é imposta somente uma das soluções (102) irá satisfazê-la; isto é, a solução assintótica aceitável para (100), será

Esta escolha prende-se também ao fato de que a função de onda Ψ(r) precisa ser quadraticamente integrável; obviamente R_l ≅ e^-ρ/2 é uma solução que não satisfaz a condição de contorno

A integral < Ψ | Ψ > = 1 deve ser interpretada como sendo a probabilidade de encontrarmos o átomo de hidrogênio contido no volume dado; “como (por definição) o átomo está contido neste dado volume, então, a probabilidade de o encontrarmos lá, é obviamente máxima, isto é, < Ψ | Ψ > = 1, uma vez que por definição, o máximo valor da probabilidade é um”. Como a função que satisfaz (100) comporta-se assintoticamente como e^-ρ/2, isto nos sugere que devemos procurar uma solução geral que seja finita, na forma de um polinômio multiplicando esta exponencial, isto é

onde f(ρ) é justamente a função polinomial a ser encontrada. Substituindo (104) na equação (100), teremos

Considerando que {ρ^k+p}∞₀ um conjunto completo, é possível então definirmos f_l(ρ) como

A função f(ρ) será definida precisamente, depois de acharmos um valor para o índice ρ e os valores dos coeficientes A_k. Para tal, nós começamos calculando f^'_l(ρ) e f^''_l(ρ), simplesmente achando as derivadas da eq. (106), isto é

Usando (106), (107) e (108) na equação (105), e rearranjando os termos, nós iremos obter a seguinte série infinita

Para k = 0, o primeiro termo de mais baixa potência de ρ em (109), será

No entanto, como é necessário que tenhamos A₀ ≠ 0 e que

então, a condição (111) só será satisfeita se

Os valores do índice ρ que satisfazem (113), são

Porém, fazendo uso de (106), a condição ρ = - ( l + 1 ) implica que

Esta solução não é fisicamente aceitável, (porque? lim f_l (ρ→0) = 0? quando p = - ( l + 1 ), f_l(ρ) é quadraticamente integrável?). Resta-nos então a solução p = l, para a qual teremos

ou ainda, utilizando a eq. (104), teremos que

Sabendo que p = l, nós podemos usar este valor na eq. (109) e obter uma série infinita de potências de ρ. Para que a soma de todos os termos desta série seja nula, é necessário que cada coeficiente de uma dada potência de ρ, seja nulo. Assim sendo, para os dois primeiros coeficientes de menor potência de ρ nós teremos:

Procedendo de forma análoga para os outros coeficientes, observaremos que todos eles obedecem à seguinte equação geral:

Analisando (118) nós observamos que se for possível conhecer A₀ nós poderemos utilizar a fórmula de recorrência (120) e calcular A₁, com A₁, calcularemos A₂ etc, até conhecermos todos os coeficientes A_k da série, para um valor qualquer de k. Porém, como a solução dada pela equação (117) deve ser finita, então a série que nela aparece deve ser finita; analisando (120) nós vemos que isto é possível desde que tenhamos

Impondo esta condição, o coeficiente do termo A_k será zero, e por conseguinte, o coeficiente A_k+1 será necessariamente nulo, assim como todos os outros coeficientes de índice ≥ k + 1, isto é, A_k+1 = A_k+3 = ... = 0.

Como k e l são números inteiros, então n será necessariamente um número inteiro. Desta forma, (117), só será uma solução da equação (97) para certos valores de k, ao qual dá-se o nome de número quântico radial, enquanto n é o número quântico total ou número quântico principal.

O número quântico principal n, não só define as possíveis funções radiais do átomo de hidrogênio, como também quantiza os valores permitidos da energia eletrônica. Isto pode ser visto através da equação (99) que define a energia eletrônica do hidrogênio, em função do número quântico principal. Fazendo uso de (99), nós então concluímos que a energia do elétron no átomo de hidrogênio, segundo a teoria de Schrödinger, é dada por

Sendo assim, nós observamos que a teoria de Schrödinger é equivalente à de Bohr, pelo menos com relação aos possíveis valores de E_n para o átomo de hidrogênio. Além do mais, como k e l podem ser 0, 1, 2 etc, então, analisando (121) nós vemos que n será necessariamente um número inteiro com valores n = 1, 2, 3, ... Porém, como n = l + k + 1, então para n = 1, teremos que l = k = 0; usando estes valores de l e k em (117), é possível definirmos R_1,0 como

onde os índices 1 e 0 representam os valores de n = 1 e l = 0. Para n = 2 podemos ter l = 0 e k = 1, ou l = 1 e k = 0.No primeiro caso teremos que

Utilizando a equação (118) para n = 2 e l = 0 poderemos calcular A₁ em função de A₀, ou seja

Consequentemente, substituindo este valor de A₁ em (124), teremos

Analogamente, para n = 2 e quando 2 = 1 e k = 0, nós teremos que

De uma maneira geral, procedendo de forma análoga nós podemos calcular R_n,l(ρ) para qualquer valor de n e l; note porém, que em todos os casos, R_n,l(ρ) depende de A₀.

Se compararmos as diferentes funções R_n,l, nós veremos que (a não ser ρ a uma constante multiplicativa envolvendo A₀) estas funções diferem muito pouco dos polinômios associados de Laguerre, L( n - l - 1 , 2l + 1 , ρ), que podem ser definidos pela seguinte fórmula geral de Rodrigues

onde m e p são números inteiros e positivos quaisquer. Consequentemente, fazendo m = n - L - 1 e p = 2l + 1, nós podemos substituir a soma que aparece em (117) pela equação (128) e definir R_n,l como

Desta forma, a constante A₀ que aparece nas funções R_1,0, R_2,0 etc que definem R_n,l, pode ser calculada se nós normalizarmos as funções R_n,l ou então utilizando a seguinte propriedade dos polinômios associados de Laguerre:

Se nós quisermos calcular A₀ normalizando as funções R_n,l então será necessário calcular a seguinte integral

Fazendo uso de (99) teremos que

onde α = 2z / na₀. Fazendo uso de (99) e (132), para fazer a mudança de variáveis em (131), nós iremos obter

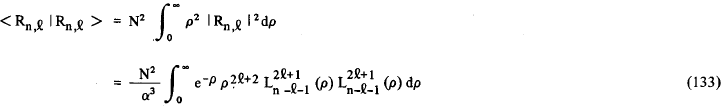
onde N é a constante de normalização das funções R_n,l = 2.Z/n.a₀. Na resolução da integral (133) nós fizemos uso da seguinte fórmula geral

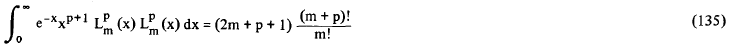
Conhecendo a constante de normalização N, nós podemos fazer uso de (129) e (134) para definir as funções R_n,l normalizadas, como:

A equação (136) pode ser reescrita em termos de r ao invés de ρ, se fizermos uso de (99); sendo assim, termos

Fig. 3. Funções de onda radiais R_n,l(r) para o átomo de hidrogênio para n = 1, 2, 3. Cada curva é designada por dois algarismos que representam os valores de n e de f. Note que para cada função existem n - f - 1 modos.