O número quântico azimutal l
A dependência em θ da função de onda Ψ é dada pela função Θ que satisfaz à equação
![]()
Antes de resolvermos (72), convém reescrevê-la e efetuar uma mudança conveniente de variável. Note que
![]()
Logo, substituindo (73) em (72) a equação diferencial para Θ pode ser reescrita como
![]()
Agora, se fizermos uma pequena e conveniente mudança de variável, isto é, definindo
![]()
então, teremos que
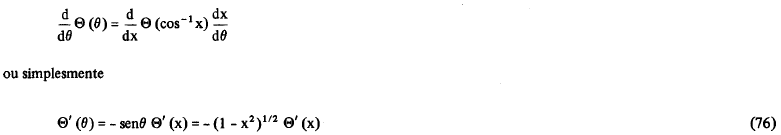
Procedendo de forma análoga, a derivada segunda de Θ será
![]()
Utilizando (75), (76) e (77) nós podemos reescrever (74), mas agora em função de x:
![]()
ou, dividindo por 1 - x2, teremos
![]()
Se agora introduzirmos uma nova função Z(x), tal que
![]()
então, teremos que
![]()
e
![]()
Substituindo (81) e (82) na equação (79), obtemos
![]()
Até o momento ainda não conseguimos achar a solução procurada; nós simplesmente definimos uma nova variável e uma nova função de tal forma a transformar a equação (72) na eq. (83). Porém, aqueles que estão familiarizados com as “equações diferenciais de Legendre”, já podem notar que a equação (83) pode ser obtida se derivarmos m vezes a equação diferencial de Legendre, definida como:
![]()
onde Pl(x) representa o polinômio de Legendre de ordem l, definido pela seguinte fórmula geral, conhecida como fórmula de Rodrigues para os polinômios de Legendre
![]()
Observe que derivando a equação (84) m vezes, obteremos
![]()
onde Pl(m+2), Pl(m+1) etc representam o polinômio de Legendre de ordem 2 derivado m + 2 vezes, m + 1 vezes, etc. Se definirmos uma nova função y(x) como
![]()
e substituirmos (87) em (86), teremos
![]()
Comparando esta equação diferencial (88) com a do nosso problema, isto é,
![]()
vemos que estas duas equações são idênticas, isto é: Z(x) = y(x) é uma solução para a equação (89) desde que a constante b, que aparece em (89), seja definida como

Desta forma, fazendo uso de (89), (88) e (87) nós podemos dizer que
![]()
Mas, com o auxílio de (91) e fazendo uso da definição de Θ(x), dada por (80), nós podemos concluir que a função Θ pode ser definida como:

Ou ainda, utilizando sub-índices em Θ(x) para indicar a dependência de Θ com l e m, teremos

A função Pl(m) é conhecida como a função de Helmholtz; a função Plm(x), que aparece em (92) é conhecida como Polinômio Associado de Legendre de ordem m.
Que é Θl,m(x)? Quando começamos a resolver a equação de Schrödinger para o átomo de hidrogênio, havíamos definido Ψ(r,θ,φ) = R Θ Φ como sendo a função de onda do hidrogênio. Logo, a função Θ que aparece nesta definição, é justamente a parte da função de onda do hidrogênio que descreve a dependência de Ψ com o ângulo θ. Note que para |m| > 2 teremos que Θl,m = 0, uma vez que P, é um polinômio de ordem l; obviamente, se derivarmos m vezes um polinômio de ordem l, e se |m| > l então a derivada de ordem m ser nula; isto é, no nosso caso
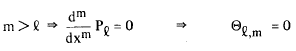
Assim, nós verificamos que os valores do módulo de m estarão restritos ao intervalo 0 ≤ |m| ≤ l. Na realidade, quando achamos Θ nós vimos que o número quântico m deveria ser nulo ou ±1, ±2 etc; porém, como o valor máximo de m depende de l, isto é |m| ≤ l, então, ao invés de m, é conveniente escrevermos ml, onde o subíndice l representa esta dependência de m com l. A função Θl,m deve ser normalizada, isto é <Θl,m | Θl,m> = 1; sendo assim, teremos que
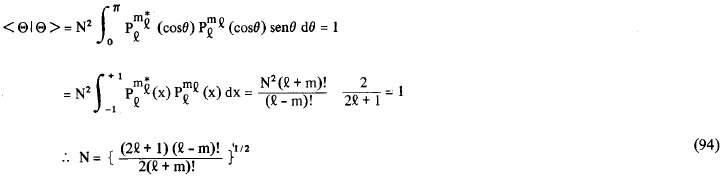 a constante de normalização N só é definida para |m| ≤ l, uma vez que não se define o fatorial de um número negativo. Finalmente concluímos que a função Θl,m(cosθ) normalizada, será
a constante de normalização N só é definida para |m| ≤ l, uma vez que não se define o fatorial de um número negativo. Finalmente concluímos que a função Θl,m(cosθ) normalizada, será
![]()
Fazendo uso de (71) e (95), a função de onda do hidrogênio pode ser escrita como

A dependência da função de onda em Θ é também quantizada, uma vez que ela só é definida para certos valores inteiros de l; l é conhecido como “número quântico azimutal”. Resta-nos agora resolvermos a equação (64) e encontrarmos uma expressão analítica para a função radial R(r).
O número magnético m
A equação que contém a dependência da função de onda em φ, pode ser resolvida facilmente pois, Φ tem que ser tal que, derivada duas vezes dê ela própria multiplicada por m2. Por inspeção da equação (62), vemos que de uma forma geral, Φ pode ser definida como
![]()
onde N é uma constante qualquer. A função (65) é uma solução aceitável, uma vez que substituída em (62) obtêm-se:
![]()
A solução mais geral de (62) seria dada pela combinação linear das soluções particulares, isto é, Φ = aeimφ+be-imφ. Porém, tomaremos como solução a exponencial com sinal positivo, ou seja
![]()
O que é Φ? É a parte da função de onda do átomo de hidrogênio que contém toda a dependência angular em φ. A função Φ deve ser normalizada à unidade (Postulado IV). Para que esta condição seja satisfeita, basta escolhermos a constante de normalização N, tal que < Φ l Φ > = 1.
Este valor de N pode ser calculado facilmente, pois

Logo, usando (66) e (67) nós podemos definir a função é normalizada, como
![]()
Além do mais, o Postulado III nos diz que Φ precisa ser unívoca, o que implica que
![]()
ou
![]()
isto é
![]()
Note que a parte imaginária da equação (70) deve ser nula ao mesmo tempo que a parte real é igual à unidade. Para que esta equação seja satisfeita, isto é, para que sen(2 π m) = 0 e ao mesmo tempo cos(2 π m) = 1, é necessário que m seja igual a 0, +1, +2, +3 etc. Ou seja, a função dada por (68) só será uma solução da equação (62) quando a constante m for igual a um destes valores discretos. Isto equivale a dizer que a dependência em φ, da função de onda total, é quantizada. A constante m é um “número quântico” denominado “número quântico magnético”. Como já conhecemos Φ, podemos dizer que Ψ(r) já pode ser escrita como
![]()
O significado do número quântico magnético e suas implicações serão discutidas mais adiante e em outras ocasiões. A seguir nós mostraremos como resolver a equação diferencial em Φ; isto nos levará naturalmente ao conceito de um novo número quântico, conhecido como “número quântico azimutal”.
A equação de Schrödinger para o átomo de hidrogênio
O átomo de hidrogênio é composto de duas partículas, o elétron e o próton. Isto significa que para resolvermos a equação de Schrödinger para o átomo de hidrogênio, nós teremos que resolver um “problema de dois corpos”. Nestes casos, o que se faz normalmente é reduzir o problema de dois corpos a um problema de um único corpo. Vejamos como isto pode ser feito.
Considere o tratamento clássico de duas partículas de massas m1 e m2, sendo m1 a massa do elétron e m2 a massa do próton. As posições destas partículas no espaço podem ser especificadas pelos vetores r1 e r2 partindo da origem de um sistema de coordenadas cartesianas, mostrado na Fig. 1. As coordenadas das partículas 1 e 2 são, respectivamente (x1, y1, z1) e (x2, y2, z2). Entre as partículas 1 e 2 nós podemos traçar o vetor r = r1 - r2, sendo que os componentes do vetor r nós chamamos de x, y e z, definidos como:
![]()
As coordenadas x, y e z são chamadas de coordenadas relativas ou coordenadas internas (vide Fig. 2). Em seguida traça-se o vetor R da origem ao ponto C, isto é, ao centro de massa do sistema. Chamando as coordenadas do centro de massa de X, Y e Z, nós definimos o vetor R como:

Fig. 1. Posicionamento do elétron e do próton do hidrogênio, utilizando coordenadas cartesianas (x, y, z) e polares esféricas (r, o e 0).

Pela definição de centro de massa para um sistema de duas partículas, podemos então definir X, Y e Z como:
![]()
As três equações (23) são equivalentes à equação
![]()
Além desta equação nós sabemos que
![]()
Considerando as equações (24) e (25) como um conjunto de equações simultâneas em função de duas variáveis r1 e r2 nós podemos então, resolver este sistema de equações e obter:
![]()
![]()
As equações (26) e (27) representam a transformação de coordenadas de x1, y1, y2 e x2, y2, z2, para x, y, z e X, Y, Z. Agora, nós já podemos lançar mão dos Postulados da mecânica quântica para escrever o Hamiltoniano para o átomo de hidrogênio, após ter feito as devidas transformações de coordenadas. Se nós representarmos a derivada de uma função em relação ao tempo por um ponto em cima da função, então a velocidade da partícula 1 pode ser definida como:
![]()
Para aplicarmos a equação de Schrödinger ao átomo de hidrogênio nós precisamos antes de mais nada escrever o hamiltoniano para ele, isto é, nós precisamos conhecer a energia cinética do hidrogênio e a função que representa o potencial de interação entre o elétron e o próton, isto é, a função V. A energia cinética T do átomo de hidrogênio, é a soma das energias cinéticas das duas partículas, isto é:
![]()
Derivando as equações (26) e (27) em relação ao tempo e substituindo estas derivadas em (29), teremos:
![]()
Lembrando a definição de um produto escalar de dois vetores, então R'-R''=|R| e r . r = |r|2. Usando estas definições, a equação (30) pode ser reescrita como
![]()
Sendo M a massa total do sistema, isto é,
![]()
então, podemos definir a massa reduzida μ do sistema de duas partículas como
![]()
Usando (32) e (33) nós podemos reescrever (31) como
![]()
O primeiro termo em (34) é a energia cinética devido ao movimento de translação de todo o sistema de massa M, isto é, do átomo de hidrogênio. O segundo termo representa a energia cinética correspondente ao movimento interno das duas partículas (elétron e próton), que formam o hidrogênio. Note que
![]()
No início das nossas discussões nós tínhamos definido seis coordenadas x1, y1, y2 e x2, y2, z2 e consequentemente podíamos definir seis momentos lineares correspondentes:
![]()
Da mesma forma, agora nós podemos comparar (29) com (34) e utilizar as seis novas coordenadas x, y, Z, X, Y, Z para definir seis novos momentos, isto é

Sendo assim, é possível então definirmos os dois novos vetores momento como
![]()
![]()
Substituindo (36) e (37) em (34) nós obtemos
![]()
Uma vez conhecida a expressão para a energia cinética do hidrogênio, nós estamos então em condições de escrever uma expressão clássica para o Hamiltoniano (energia cinética + potencial) deste átomo. Como o potencial de interação V, entre o elétron e o próton, é puramente coulômbico, teremos que:
![]()
onde Z é o número atômico do átomo, -e2 é o produto das cargas e (x2 + y2 + z2) é a distância entre o elétron e o próton, neste novo sistema de coordenadas, onde o próton encontra-se na origem. Logo, conhecendo T e V nós podemos fazer uso de (38) e (39) para escrever H, o Hamiltoniano do sistema:

Usando os Postulados da mecânica quântica, nós podemos substituir os componentes dos momentos pelos seus respectivos operadores e obter a seguinte equação de Schrödinger para o átomo de hidrogênio:

Isto é possível, uma vez que o sistema é conservativo, pois o potencial não depende do tempo. Nestas equações ET é a energia total do átomo, isto é, energia cinética mais energia potencial e os símbolos x e X são usados simplesmente para representarem o conjunto de coordenadas x, y, z e X, Y, Z, respectivamente. Se agora assumirmos que a função Ψ pode ser definida como
![]()
e se substituirmos (42) em (41) iremos obter
![]()
Dividindo ambos os lados da equação pelo produto ΨΦ, teremos
![]()
Note porém que (44) é uma equação diferencial composta pela soma de duas outras independentes entre si. Assim, podemos supor que
![]()
Considerando que a energia total ET é constante, então é possível separarmos a equação diferencial (44) em duas outras:
![]()
![]()
A equação diferencial (46) é a equação de Schrödinger para uma partícula de massa M = m1 + m2 que se desloca no espaço, livre da ação de um campo de potencial (isto é Vcg = 0) ou, o que é equivalente, sob a ação de um campo de potencial constante que no caso é nulo: ela é a equação de Schrödinger para uma “partícula livre” e de massa M. Toda sua energia Ecg aparece sob a forma de energia cinética. A segunda equação diferencial, isto é, eq. (47), é a equação de Schrödinger para o elétron do átomo de hidrogênio. Este elétron teve sua massa corrigida de m, para μ = ( m1 m2 ) / M. A energia potencial V(x) é dada simplesmente pela interação coulômbica do elétron com o próton do núcleo, isto é
![]() onde r é a distância entre o elétron e o próton e Z é número de cargas do núcleo, número atômico (no caso do hidrogênio Z=1). Neste caso, o campo de potencial dado por V(x) é isotrópico e varia simplesmente com o inverso da distância entre o elétron e o núcleo; este é um caso típico de problema de uma partícula sob a ação de um campo central. No momento nós não estamos interessados no movimento de uma partícula livre no espaço mas sim, na equação que descreve o comportamento do elétron no átomo. Por conseguinte, deixaremos a eq. (46) para ser discutida em outra ocasião e iremos concentrar a nossa atenção na eq. (47); assim, a equação que representa o elétron no átomo de hidrogênio pode ser escrita como
onde r é a distância entre o elétron e o próton e Z é número de cargas do núcleo, número atômico (no caso do hidrogênio Z=1). Neste caso, o campo de potencial dado por V(x) é isotrópico e varia simplesmente com o inverso da distância entre o elétron e o núcleo; este é um caso típico de problema de uma partícula sob a ação de um campo central. No momento nós não estamos interessados no movimento de uma partícula livre no espaço mas sim, na equação que descreve o comportamento do elétron no átomo. Por conseguinte, deixaremos a eq. (46) para ser discutida em outra ocasião e iremos concentrar a nossa atenção na eq. (47); assim, a equação que representa o elétron no átomo de hidrogênio pode ser escrita como
![]()
ou mais explicitamente
![]()
A equação (50) é comumente conhecida como a equação de Schrödinger para o átomo de hidrogênio (quando Z = 1), onde E é a energia eletrônica total do elétron do átomo de hidrogênio. Resolver a equação de Schrödinger significa achar uma fórmula analítica ou numérica para a função de onda. Em geral, a resolução da equação de Schrödinger é bastante difícil.
Na realidade, somente para poucos casos é que conhecemos soluções analíticas exatas para esta equação. No que diz respeito a átomos, até o presente momento, só conhecemos soluções exatas para sistemas com um único elétron como é o caso do átomo de hidrogênio; entre as moléculas, um exemplo é o íon H2+ para o qual as soluções exatas são conhecidas. Em outras palavras, somente conhecemos soluções analíticas exatas para sistemas atômicos e moleculares que possuem um único elétron. A esta altura só nos resta resolver a equação de Schrödinger para o hidrogênio, isto é, achar a função de onda ψ(x) para o hidrogênio. Como o átomo de hidrogênio tem simetria esférica então será conveniente trabalharmos com Coordenadas Polares Esféricas ao invés de Coordenadas Cartesianas. Utilizando as relações abaixo

Fig. 2. Coordenadas internas para o elétron do átomo de hidrogênio. Neste sistema o próton encontra-se na origem. A massa do próton é cerca de 1800 vezes maior do que a do elétron e por esta razão o centro de massa do sistema está muito próximo do próton.

podemos mostrar que o operador Laplaciano ∇2 neste novo sistema de coordenadas será
![]()
Representando o conjunto de coordenadas r, θ, Φ por r, nós podemos reescrever a equação de Schrödinger para o hidrogênio como
![]()
De agora em diante o nosso objetivo será achar a função Ψ(r) que satisfaz a equação diferencial (53). Para tal, nós supomos que v(r) pode ser representada por um produto de três funções, isto é
![]()
Com isto nós estamos supondo que a função R só depende de r, e que as funções Θ e Φ só dependem de θ e φ, respectivamente. Substituindo (54) em (53), teremos
![]()
Dividindo toda a equação (55) pelo produto R(r) Θ(θ) Φ(φ) e rearranjado, teremos que
![]() Ora, como esta equação diferencial (56), na realidade é composta por três outras, isto é, uma que só depende de r, outra em θ, e outra em φ, então é conveniente desmembrá-la em três outras equações: para tal, basta multiplicarmos tudo por r2sen2θ e rearranjarmos os termos obtidos. Fazendo isto, obtemos:
Ora, como esta equação diferencial (56), na realidade é composta por três outras, isto é, uma que só depende de r, outra em θ, e outra em φ, então é conveniente desmembrá-la em três outras equações: para tal, basta multiplicarmos tudo por r2sen2θ e rearranjarmos os termos obtidos. Fazendo isto, obtemos:
![]()
Na eq. (57), r, θ e φ são variáveis independentes; porém, como o lado esquerdo desta equação depende de r e θ, e é igual a uma equação que só depende de φ, então é óbvio que esta igualdade só poderá ser satisfeita quando ambos os lados forem iguais a uma constante que por conveniência chamaremos de -m2. Matematicamente esta constante é chamada de constante de separação. Sendo assim, teremos que
![]()
Lembrando que o potencial só depende de r, nós podemos então separar a equação (58) em duas outras, isto é
![]()
e
![]()
Entretanto reescrevendo a equação (59) e procedendo de forma análoga nós iremos obter
![]()
Sendo que neste caso a constante de separação é -b. Usando (60) e (61) nós podemos dizer que todo o nosso problema de encontrar a solução da equação de Schrödinger resume-se na procura das funções R, Θ e Φ que satisfazem as equações
![]()
![]()
![]()
Uma vez resolvidas estas equações nós teremos encontrado que nada mais é do que o produto R Θ Φ e teremos, então, a função de onda que descreve o comportamento do elétron no átomo de H. Veremos também que como consequência, nós iremos encontrar três constantes que serão os números quânticos.
Postulados da Mecânica Quântica
I. A todo sistema corresponde uma função de onda Ψ(x t).
II. A seguinte correspondência existe entre as variáveis dinâmicas e os seguintes operadores:
| variáveis | operadores | |
| x,y,z,t | → | x,y,z,t |
| f(x,t) | → | f(x,t) |
![]()
![]()
Assim, se substituirmos as variáveis acima pelos seus operadores equivalentes, podemos utilizar uma fórmula clássica e adaptá-la à nova linguagem. Por exemplo, utilizando as equações clássicas de movimento de Hamilton, podemos mostrar que o Hamiltoniano H para um sistema conservativo é dado por
H = T + V = E
onde E é a energia total do sistema e T e V são energias cinética e potencial, respectivamente. Uma força é conservativa se o trabalho W(A→B) feito pela força para mover um corpo de A→B, for independente do caminho seguido para ir de A a B. Um campo de força central (isto é, um campo cuja grandeza é função somente da distância do centro) é um exemplo de sistema conservativo. Sendo p o momento do sistema e sendo V a sua energia potencial que depende das coordenadas x, y e z, isto é V = V(x,y,z), então teremos,
![]()
onde p é o momento e m é a massa da partícula. Usando as regras acima, o Hamiltoniano pode ser reescrito como
![]()
ou
![]()
Esta é a equação de Schrödinger para um sistema de 4 dimensões: três espaciais e uma temporal. O primeiro termo do lado esquerdo desta última equação representa o operador correspondente à energia cinética do sistema, e o segundo termo representa a energia potencial do mesmo.
III. Ψ(x,t) (onde x representa x, y, z) e suas derivadas primeiras, devem ser contínuas, finitas e unívocas.
IV. Ψ(x,t) deve ser normalizada, isto é


O símbolo dv que aparece nas equações acima representa o elemento de volume: em coordenadas cartesianas dv = dx dy dz. V. A cada observável corresponde um operador A. O valor médio <A> ou valor esperado deste operador é definido como

Porém, se Ψ não for normalizada, então <A> é definido como
![]()
Muitas vezes nós usaremos a notação <Ψ|A|Ψ> e não <Ψ|AΨ>; no entanto ambas as notações possuem o mesmo significado. Desta forma, se conhecermos a. função de onda de um sistema nós podemos calcular “praticamente” quase tudo a respeito dele.
