O átomo de hidrogênio ocupa um certo volume no espaço; obviamente o elétron acha-se completamente contido neste volume, e como consequência disto, a probabilidade, ou melhor, a probabilidade total de encontrarmos este elétron neste dado volume é máxima, isto é, se calcularmos esta probabilidade ela deverá ser igual à unidade. Vimos que, sendo Ψnlm a função de onda que representa o comportamento do elétron do átomo de hidrogênio, então a probabilidade total de encontrarmos o elétron do hidrogênio (na região do espaço que o átomo existe) é definida como:
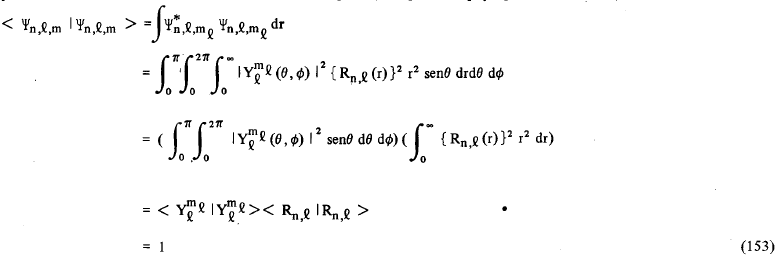
Na integral (153), dr representa o elemento de volume em coordenadas polares esféricas, isto é, dr = r2 sen(θ) dr dθ dφ. Muitas vezes nós representamos o elemento de volume por dv ao invés de dr. Se, ao invés da probabilidade total nós quisermos calcular a probabilidade de encontrar o elétron em uma dada região do espaço compreendida entre r e r + dr; θ e θ + dθ; e φ e φ + dφ; basta calcularmos
![]()
Esta fórmula é exatamente equivalente ao integrando da equação (153), e corresponde à probabilidade de encontrarmos o elétron no elemento de volume dr= r2 sen(θ) dr dθ dφ.
Tabela 2. Funções Reais para o elétron do átomo de hidrogênio.

Por outro lado, a probabilidade de encontrarmos um elétron numa região esférica tendo o núcleo como centro das coordenadas r e de raio externo r + dr, e independente de θ e φ, é dada por
![]()
À função {Rn,l(r)}2.r2 dá-se o nome de Função de Distribuição Radial, D(r); {Rn,l(r)}2.r2 nos dá a probabilidade de encontrar o elétron a uma distância r do núcleo.
Fig. 6. Função de distribuição radial D(r), para o átomo de hidrogênio para valores de m = 1, 2 e 3. A seta indica o valor de <r>nlm.
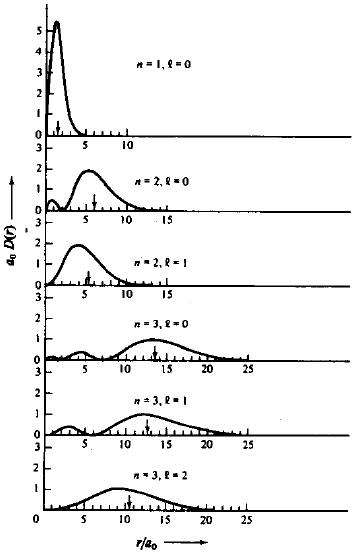
A função D(r) representa a probabilidade de encontrarmos o elétron à uma dada distância r do núcleo. Analisando o comportamento de D(r), para o elétron no orbital 1s, veremos que à medida que fazemos r variar de zero a ∞, D(r) que inicialmente é zero, passa por um máximo para depois decair novamente para zero. O valor de r para o qual D(r) é máxima, corresponde exatamente ao valor de r que mais contribui para o valor médio < r >. Este valor de r para o qual D(r) é máxima, corresponde ao “raio de Bohr”, que aliás difere do valor esperado < r > ou valor médio de r no estado fundamental. O ponto em que D(r) passa por um máximo pode ser calculado facilmente, pois neste ponto d / dr {D(r)} = 0. Assim, para o orbital 1s, teremos que

Isto quer dizer que a função de distribuição radial, para o H no estado 1s, passa por um máximo no ponto em que r = 0,529Ao; este valor é exatamente igual ao valor calculado por Bohr. Note que o elétron do átomo de Bohr circulava numa órbita plana de raio r = 0,529Ao, enquanto que neste caso temos simetria esférica. A diferença entre o valor médio de r e o valor de r = a0 determinado por Bohr, pode ser demonstrada facilmente. Como a função de onda para o hidrogênio é normalizada, o valor esperado ou valor médio para o raio r do átomo de hidrogênio quando está no estado fundamental (i. e., 1s), é dado por (vide postulado V).
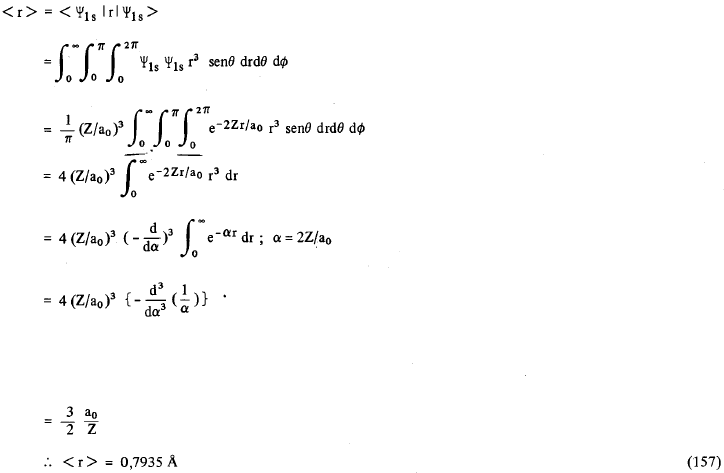
Isto quer dizer que se determinarmos r experimentalmente, isto é, se pudermos medir o “raio” do átomo de hidrogênio no estado fundamental (orbital 1s), veremos que este valor experimental coincide com < r >= 0,793Ao e não com 0,529Ao. De uma maneira geral, o valor médio de r, isto é < r >n,l é dado por

Assim, analisando (158) nós vemos que em média quanto maior for o número quântico principal n, mais afastado do próton estará o elétron. No estado fundamental do hidrogênio (n = 1, l = 0), o elétron encontra-se em média a 3/2 a0 do núcleo, o que está de acordo com o que já havíamos calculado anteriormente.
