Inicialmente nós havíamos definido Ψ como um produto das funções R, Θ e Φ. Sendo assim, fazendo uso de (68), (95) e (137), nós podemos definir a função de onda eletrônica do átomo de hidrogênio, como:

ou ainda
![]()
onde as funções Yl,m (θ,φ) são conhecidas como Harmônicos Esféricos, e definidas como

Como os conjuntos de funções {Φm}, {Θl,m} e {Rn,l} são ortogonais, então a função Ψ será também ortogonal.
Resumindo estas propriedades, teremos:
![]()
![]()

Agora que conhecemos a solução da Equação de Schrödinger para o átomo de hidrogênio, já estamos em condições de definir e estudar uma série de propriedades relacionadas com o mesmo. As funções de onda para o hidrogênio (ou para átomos ou íons atômicos com um único elétron) são definidas através de (138) fórmula geral para Ψnlm. Cada conjunto de n, l, m define uma função de onda, que por sua vez representa um dado estado eletrônico do átomo. Quando n é igual a um, nós dizemos que o elétron está na camada K. As camadas eletrônicas K, L, M, etc., correspondem respectivamente a n = 1,2,3 etc. As funções de onda de um único elétron são comumente chamadas de orbitais. Assim, não é correto referir-se a “orbitais de dois elétrons”. Orbitais correspondentes a l = 0, 1, 2, 3, 4, 5 etc, são conhecidos respectivamente, por orbitais s, p, d, f, g, h, etc., omitindo-se somente a letra j. Assim, a função de onda correspondente a n=2, l = 1, m = 0 é representada por Ψ2,1,0 ou simplesmente, função 2p. A designação destas letras (s, p, d, f, g, etc.) prende-se à terminologia inglesa utilizada por espectroscopistas que distinguiam linhas espectrais pelo seu aspecto, isto é, s → sharp, p → principal, d → difuse e f → fine. As outras foram sugeridas como extensão da nomenclatura, mantendo a ordem alfabética.
Na Tabela 1 nós temos as fórmulas de algumas funções de onda eletrônicas para estados estacionários do hidrogênio.
Tabela 1 - Funções de onda para o hidrogênio. Nestas equações σ = nρ / 2 = Zr/a0. Os sinais superiores e inferiores nos índices de Ψ devem corresponder respectivamente aos sinais superiores ou inferiores da parte exponencial das fórmulas. Neste caso, todos os índices positivos de Ψ correspondem a exp(imφ) e os negativos correspondem a exp(-imφ).

Figura 4 - Gráficos polares dos Harmônios Esféricos para l = 0, 1, 2 para todos os valores do índice m e para φ = 0. A linha tracejada indica o eixo z.

Através da equação (138) que define Ψnlm nós podemos notar que, com exceção dos casos em que m = 0, todas as funções hidrogênicas são complexas, isto é, possuem uma parte imaginária, não nula, Comumente, quando discutimos os problemas relacionados com estrutura atômica, molecular e ligações químicas, utilizamos funções hidrogênicas reais obtidas pela combinação linear destas funções complexas. Assim, para n = 2 e l = 1 podemos definir as funções reais Ψ2px, Ψ2py e Ψ2pz como
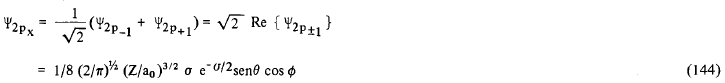

![]()
O fator de 1 / √2 que aparece nas definições de 2px e 2py é simplesmente uma constante de normalização que poderia ser calculada facilmente, caso nós não a tivéssemos definido de antemão. Para tal, bastaria escrevermos Ψpx, como
![]()
e calcular o produto escalar impondo a condição de que < Ψ2px | Ψ2py> = 1. Assim, lembrando que as funções Ψn,l,m. São ortonormalizadas, isto é
![]()
teremos que
![]()
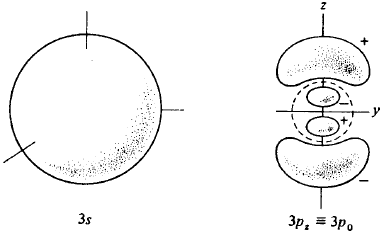
Fig. 5. Formato de alguns orbitais atômicos do átomo de hidrogênio. O orbital 2s tem um modo esférico que não aparece na figura; O orbital 3s tem dois destes modos. O orbital 3p, tem um modo esférico (indicado pela linha tracejada) e um plano modal (o plano xy). O orbital 3dz2 tem dois cones modais e o 3dx2-y2 tem dois planos modais. Na figura nós indicamos os sinais relativos de cada função de onda.


Existe uma razão muito simples para a designação destas funções como 2px, 2py e 2pz. Lembrando que podemos reescrever as funções Ψ2px, Ψ2py e Ψ2pz como
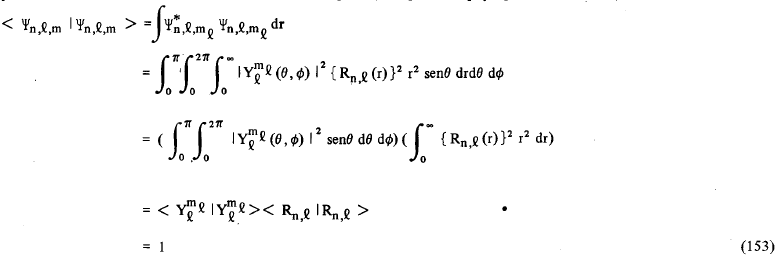
Note que x, y e z aparecem respectivamente nas definições de 2px, 2py e 2pz, dando origem a esta notação. As fórmulas para algumas destas funções reais, desde 1s até 3dxy, são dadas na Tabela 2, na qual explicitamos ao lado de cada uma a sua dependência com as coordenadas cartesianas a fim de tornar mais claro o simbolismo empregado.
