A função R(r) é a solução da equação diferencial (64) e nos dá a dependência radial da função de onda do átomo de hidrogênio. Se nesta equação substituirmos a constante b pelo seu valor, então (64) pode ser reescrita como
![]()
ou então
![]()
Para resolvermos esta equação, convém efetuarmos algumas mudanças de variáveis, definindo
![]()
onde n é uma constante qualquer, a ser determinada, utilizando (99) nós podemos reescrever (98) como:
![]()
Para resolvermos a equação diferencial (100) nós utilizaremos um método diferente daqueles empregados para as equações em θ e φ. Neste caso nós iniciaremos o nosso estudo fazendo uma análise do comportamento assintótico (para valores grandes de p) da equação radial; assim, no limite do p →∞, a equação diferencial (100) reduz-se a
![]()
cujas soluções são
![]()
Considerando que um átomo é finito, então a função Rl(p) deve ser tal que
![]()
Obviamente, quando esta condição é imposta somente uma das soluções (102) irá satisfazê-la; isto é, a solução assintótica aceitável para (100), será
![]()
Esta escolha prende-se também ao fato de que a função de onda Ψ(r) precisa ser quadraticamente integrável; obviamente Rl ≅ e-ρ/2 é uma solução que não satisfaz a condição de contorno
![]()
A integral < Ψ | Ψ > = 1 deve ser interpretada como sendo a probabilidade de encontrarmos o átomo de hidrogênio contido no volume dado; “como (por definição) o átomo está contido neste dado volume, então, a probabilidade de o encontrarmos lá, é obviamente máxima, isto é, < Ψ | Ψ > = 1, uma vez que por definição, o máximo valor da probabilidade é um”. Como a função que satisfaz (100) comporta-se assintoticamente como e-ρ/2, isto nos sugere que devemos procurar uma solução geral que seja finita, na forma de um polinômio multiplicando esta exponencial, isto é
![]()
onde f(ρ) é justamente a função polinomial a ser encontrada. Substituindo (104) na equação (100), teremos
![]()
Considerando que {ρk+p}∞0 um conjunto completo, é possível então definirmos fl(ρ) como
![]()
A função f(ρ) será definida precisamente, depois de acharmos um valor para o índice ρ e os valores dos coeficientes Ak. Para tal, nós começamos calculando f'l(ρ) e f''l(ρ), simplesmente achando as derivadas da eq. (106), isto é
![]()
![]()
Usando (106), (107) e (108) na equação (105), e rearranjando os termos, nós iremos obter a seguinte série infinita
![]()
Para k = 0, o primeiro termo de mais baixa potência de ρ em (109), será
![]()
No entanto, como é necessário que tenhamos A0 ≠ 0 e que
![]()
então, a condição (111) só será satisfeita se
![]()
![]()
Os valores do índice ρ que satisfazem (113), são
![]()
Porém, fazendo uso de (106), a condição ρ = - ( l + 1 ) implica que
![]()
Esta solução não é fisicamente aceitável, (porque? lim fl (ρ→0) = 0? quando p = - ( l + 1 ), fl(ρ) é quadraticamente integrável?). Resta-nos então a solução p = l, para a qual teremos
![]()
ou ainda, utilizando a eq. (104), teremos que
![]()
Sabendo que p = l, nós podemos usar este valor na eq. (109) e obter uma série infinita de potências de ρ. Para que a soma de todos os termos desta série seja nula, é necessário que cada coeficiente de uma dada potência de ρ, seja nulo. Assim sendo, para os dois primeiros coeficientes de menor potência de ρ nós teremos:
![]()
![]()
Procedendo de forma análoga para os outros coeficientes, observaremos que todos eles obedecem à seguinte equação geral:
![]()
Analisando (118) nós observamos que se for possível conhecer A0 nós poderemos utilizar a fórmula de recorrência (120) e calcular A1, com A1, calcularemos A2 etc, até conhecermos todos os coeficientes Ak da série, para um valor qualquer de k. Porém, como a solução dada pela equação (117) deve ser finita, então a série que nela aparece deve ser finita; analisando (120) nós vemos que isto é possível desde que tenhamos

Impondo esta condição, o coeficiente do termo Ak será zero, e por conseguinte, o coeficiente Ak+1 será necessariamente nulo, assim como todos os outros coeficientes de índice ≥ k + 1, isto é, Ak+1 = Ak+3 = ... = 0.
Como k e l são números inteiros, então n será necessariamente um número inteiro. Desta forma, (117), só será uma solução da equação (97) para certos valores de k, ao qual dá-se o nome de número quântico radial, enquanto n é o número quântico total ou número quântico principal.
O número quântico principal n, não só define as possíveis funções radiais do átomo de hidrogênio, como também quantiza os valores permitidos da energia eletrônica. Isto pode ser visto através da equação (99) que define a energia eletrônica do hidrogênio, em função do número quântico principal. Fazendo uso de (99), nós então concluímos que a energia do elétron no átomo de hidrogênio, segundo a teoria de Schrödinger, é dada por

Sendo assim, nós observamos que a teoria de Schrödinger é equivalente à de Bohr, pelo menos com relação aos possíveis valores de En para o átomo de hidrogênio. Além do mais, como k e l podem ser 0, 1, 2 etc, então, analisando (121) nós vemos que n será necessariamente um número inteiro com valores n = 1, 2, 3, ... Porém, como n = l + k + 1, então para n = 1, teremos que l = k = 0; usando estes valores de l e k em (117), é possível definirmos R1,0 como
![]()
onde os índices 1 e 0 representam os valores de n = 1 e l = 0. Para n = 2 podemos ter l = 0 e k = 1, ou l = 1 e k = 0.No primeiro caso teremos que
![]()
Utilizando a equação (118) para n = 2 e l = 0 poderemos calcular A1 em função de A0, ou seja
![]()
Consequentemente, substituindo este valor de A1 em (124), teremos
![]()
Analogamente, para n = 2 e quando 2 = 1 e k = 0, nós teremos que
![]()
De uma maneira geral, procedendo de forma análoga nós podemos calcular Rn,l(ρ) para qualquer valor de n e l; note porém, que em todos os casos, Rn,l(ρ) depende de A0.
Se compararmos as diferentes funções Rn,l, nós veremos que (a não ser ρ a uma constante multiplicativa envolvendo A0) estas funções diferem muito pouco dos polinômios associados de Laguerre, L( n - l - 1 , 2l + 1 , ρ), que podem ser definidos pela seguinte fórmula geral de Rodrigues
![]()
onde m e p são números inteiros e positivos quaisquer. Consequentemente, fazendo m = n - L - 1 e p = 2l + 1, nós podemos substituir a soma que aparece em (117) pela equação (128) e definir Rn,l como
![]()
Desta forma, a constante A0 que aparece nas funções R1,0, R2,0 etc que definem Rn,l, pode ser calculada se nós normalizarmos as funções Rn,l ou então utilizando a seguinte propriedade dos polinômios associados de Laguerre:
![]()
Se nós quisermos calcular A0 normalizando as funções Rn,l então será necessário calcular a seguinte integral
![]()
Fazendo uso de (99) teremos que

onde α = 2z / na0. Fazendo uso de (99) e (132), para fazer a mudança de variáveis em (131), nós iremos obter
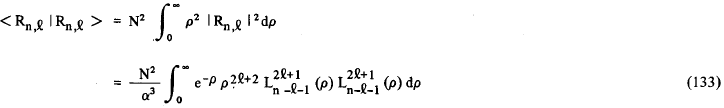

onde N é a constante de normalização das funções Rn,l = 2.Z/n.a0. Na resolução da integral (133) nós fizemos uso da seguinte fórmula geral
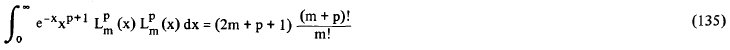
Conhecendo a constante de normalização N, nós podemos fazer uso de (129) e (134) para definir as funções Rn,l normalizadas, como:
![]()
A equação (136) pode ser reescrita em termos de r ao invés de ρ, se fizermos uso de (99); sendo assim, termos

Fig. 3. Funções de onda radiais Rn,l(r) para o átomo de hidrogênio para n = 1, 2, 3. Cada curva é designada por dois algarismos que representam os valores de n e de f. Note que para cada função existem n - f - 1 modos.

