A dependência em θ da função de onda Ψ é dada pela função Θ que satisfaz à equação
Antes de resolvermos (72), convém reescrevê-la e efetuar uma mudança conveniente de variável. Note que
Logo, substituindo (73) em (72) a equação diferencial para Θ pode ser reescrita como
Agora, se fizermos uma pequena e conveniente mudança de variável, isto é, definindo
então, teremos que
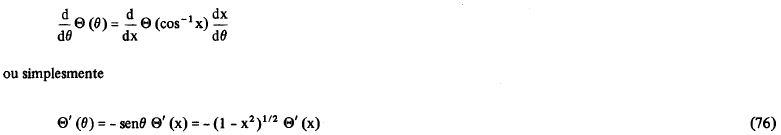
Procedendo de forma análoga, a derivada segunda de Θ será
Utilizando (75), (76) e (77) nós podemos reescrever (74), mas agora em função de x:
ou, dividindo por 1 - x2, teremos
Se agora introduzirmos uma nova função Z(x), tal que
então, teremos que
e
Substituindo (81) e (82) na equação (79), obtemos
Até o momento ainda não conseguimos achar a solução procurada; nós simplesmente definimos uma nova variável e uma nova função de tal forma a transformar a equação (72) na eq. (83). Porém, aqueles que estão familiarizados com as “equações diferenciais de Legendre”, já podem notar que a equação (83) pode ser obtida se derivarmos m vezes a equação diferencial de Legendre, definida como:
onde Pl(x) representa o polinômio de Legendre de ordem l, definido pela seguinte fórmula geral, conhecida como fórmula de Rodrigues para os polinômios de Legendre
Observe que derivando a equação (84) m vezes, obteremos
onde Pl(m+2), Pl(m+1) etc representam o polinômio de Legendre de ordem 2 derivado m + 2 vezes, m + 1 vezes, etc. Se definirmos uma nova função y(x) como
e substituirmos (87) em (86), teremos
Comparando esta equação diferencial (88) com a do nosso problema, isto é,
vemos que estas duas equações são idênticas, isto é: Z(x) = y(x) é uma solução para a equação (89) desde que a constante b, que aparece em (89), seja definida como
Desta forma, fazendo uso de (89), (88) e (87) nós podemos dizer que
Mas, com o auxílio de (91) e fazendo uso da definição de Θ(x), dada por (80), nós podemos concluir que a função Θ pode ser definida como:
Ou ainda, utilizando sub-índices em Θ(x) para indicar a dependência de Θ com l e m, teremos
A função Pl(m) é conhecida como a função de Helmholtz; a função Plm(x), que aparece em (92) é conhecida como Polinômio Associado de Legendre de ordem m.
Que é Θl,m(x)? Quando começamos a resolver a equação de Schrödinger para o átomo de hidrogênio, havíamos definido Ψ(r,θ,φ) = R Θ Φ como sendo a função de onda do hidrogênio. Logo, a função Θ que aparece nesta definição, é justamente a parte da função de onda do hidrogênio que descreve a dependência de Ψ com o ângulo θ. Note que para |m| > 2 teremos que Θl,m = 0, uma vez que P, é um polinômio de ordem l; obviamente, se derivarmos m vezes um polinômio de ordem l, e se |m| > l então a derivada de ordem m ser nula; isto é, no nosso caso
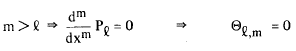
Assim, nós verificamos que os valores do módulo de m estarão restritos ao intervalo 0 ≤ |m| ≤ l. Na realidade, quando achamos Θ nós vimos que o número quântico m deveria ser nulo ou ±1, ±2 etc; porém, como o valor máximo de m depende de l, isto é |m| ≤ l, então, ao invés de m, é conveniente escrevermos ml, onde o subíndice l representa esta dependência de m com l. A função Θl,m deve ser normalizada, isto é <Θl,m | Θl,m> = 1; sendo assim, teremos que
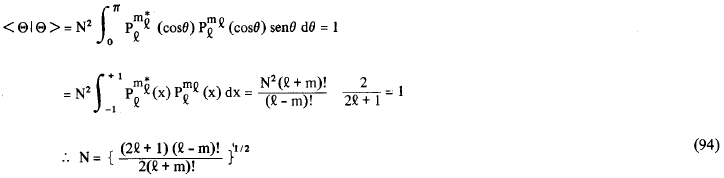a constante de normalização N só é definida para |m| ≤ l, uma vez que não se define o fatorial de um número negativo. Finalmente concluímos que a função Θl,m(cosθ) normalizada, será
Fazendo uso de (71) e (95), a função de onda do hidrogênio pode ser escrita como
A dependência da função de onda em Θ é também quantizada, uma vez que ela só é definida para certos valores inteiros de l; l é conhecido como “número quântico azimutal”. Resta-nos agora resolvermos a equação (64) e encontrarmos uma expressão analítica para a função radial R(r).